Research
CRC 1456 Mathematics of experiment
- Project B06: Compensating motion and model inexactness in nano-CT and local tomography (with Tim Salditt)
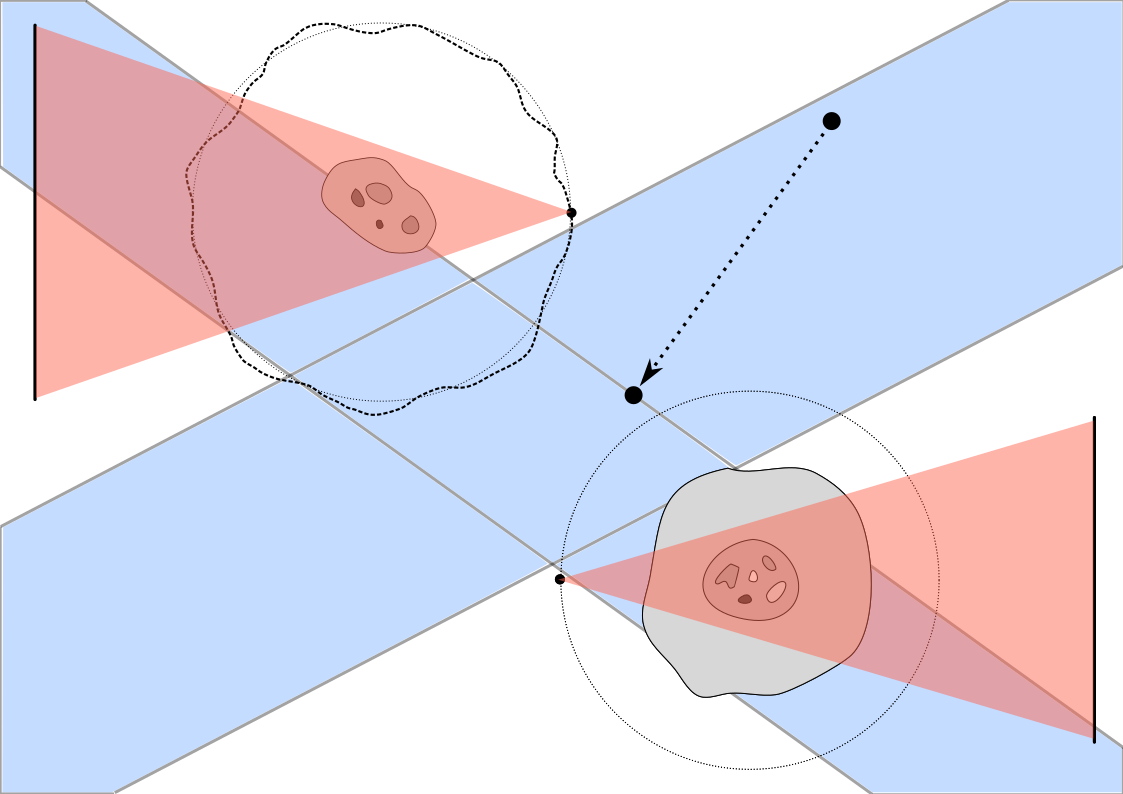
Tomographic imaging with X-rays on the nano scale requires to overcome several hurdles such as a relative motion between the scanner and the object as well as the presence of unknown material outside the targeted region of interest. In this project, we aim at using simplified mathematical models and develop strategies to compensate the resulting modelling errors by means of analytical, statistical as well as data-driven techniques to obtain efficient and precise imaging algorithms specifically suited for nano-CT imaging.
RTG 2756 Cytoskeletal elements of active matter – from molecular interactions to cellular biophysics (CYTAC)
- Project A4: Multiscale rheological inverse problems and active processes in cells
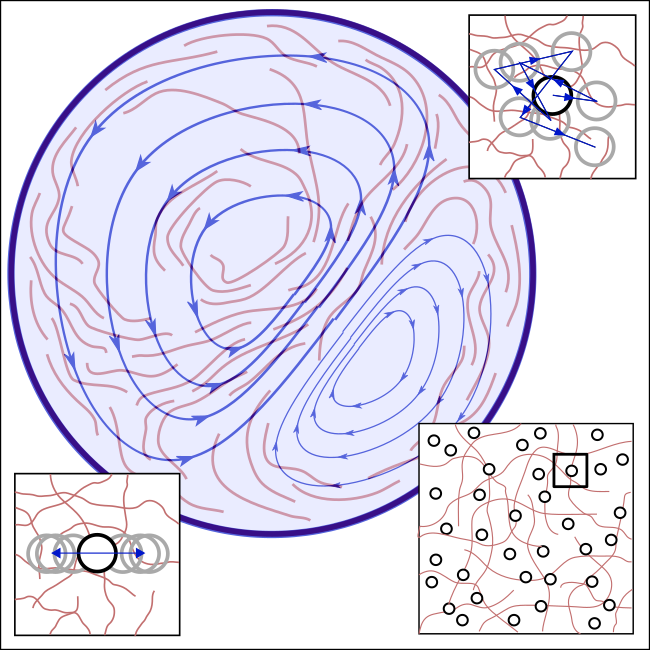
The determination of mechanical properties, such as the viscosity, of active matter usually requires the evaluation of indirect measurement data, since the respective parameters cannot be determined directly. Mathematically, such problems are called inverse problems: we want to reconstruct an unknown quantity from its impact on an observable quantity, where the measurements are usually noisy. The goal of this project is to formulate, analyze and solve inverse problems arising in rheological experiments on multiple scales. The experiments conducted in project A6 of RTG 2756 serve as a main application: Observations of the flow field inside actomyosin droplets caused by the interacting proteins are used to determine their cause, summarized as an active force density, along with a potentially heterogeneous viscosity and properties of the actomyosin network.
General research areas:
- Nonlinear and time-dependent inverse problems:
- analysis and regularization
- examples: Terahertz tomography, determination of material parameters (e.g., refractive index, viscosity)
- Machine learning for solving inverse problems:
- post-processing in computerized tomography
- partly learned solution methods
- Parameter identification for partial differential equations:
- analysis of parameter identification problems
- examples: determination of viscosity and active force densities for the Stokes equation in cell physics
- Tomographic imaging:
- terahertz tomography
- (dynamic) computerized tomography (CT), in particular nano-CT
- magnetic particle imaging
- Regularization methods:
- stable solution of inverse problems from noisy data
- example: sequential subspace optimization
- combination with deep learning techniques (hybrid methods)
- Inverse problems with inexact forward operator:
- compensation of modelling errors during regularization
- estimation of inexactness
- particularly: time-dependent modelling errors
